Лаб. 11. Термомеханики и прочности новых материалов

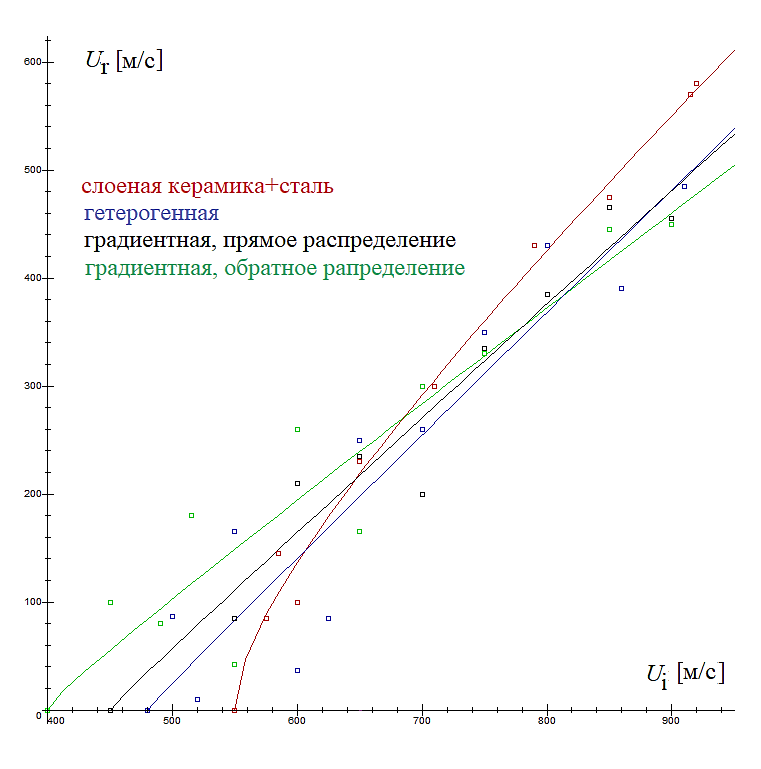
1. В численном эксперименте показано преимущество в бронестойкости гетерогенных и градиентных преград из керамики В₄С и стали перед двухслойной преградой из тех же материалов при скорости взаимодействия, превышающей 650 м/с.

Предложен подход для численного моделирования поведения гетерогенных и градиентных сред в динамических условиях на основе случайного распределения концентрации керамики по объему стальной пластины (рис. 1).

Численные эксперименты по расчету процессов проникания ударника из закаленной стали в преграды, построенные из различных комбинаций керамики В₄С и мягкой стали, показали преимущество в стойкости последних перед двухслойной преградой из пластин керамики В₄С и стали при скоростях встречи превышающих 650 м/с.

Баллистические кривые преград из гетерогенных, градиентных материалов и двухслойной преграды, состоящей из пластин керамики В₄С и стали.

U_r, U_i – остаточная и начальная скорости.

 

Ответственные исполнители: зав. лаб., к.ф.-м.н. Краус Е.И. (2018 г.).

2. При условии совместности деформаций построена замкнутая упругопластическая модель, описывающая распространение ударных волн в металлокерамических композитах. Установлено, что скорость распространения волны сжатия в композите пропорциональна объемной концентрации компонент и для предела текучести справедливо правило аддитивности смеси по массам.

Моделирование металлокерамического композита проводилось с помощью случайного распределения компонент композита по заданной концентрации. Осреднение величин для заданной концентрации компонент смеси осуществлялось вдоль распространения упругопластической волны сжатия.

 

Фрагмент модели смесевого материала из никеля Ni и карбида бора B4C	Фрагмент модели смесевого материала из никеля Ni и карбида бора B4C

Ответственные исполнители: зав. лаб., к.ф.-м.н. Краус Е.И., с.н.с. к.ф.-м.н. Шабалин И.И. (2017 г.).

3. Впервые создан метод получения неразъемного соединения современного авиационного материала — алюминиевого сплава 1424 (Al–Mg–Li). Метод основан на комплексном подходе, включающем лазерную сварку в режиме кинжального проплавления, с последующим пластическим деформированием сварного шва. При прочности основного материала 460 МПа и прочности сварного шва, полученного традиционным методом, около 360 МПа, применение нового комплексного подхода позволило увеличить прочность неразъемного соединения до 440 МПа, то есть увеличить ее на 22% и приблизиться к уровню 0,95 от прочности основного металла. Разработанный метод открывает перспективу создания технологии автоматической лазерной сварки корпусов пассажирских самолетов, что невозможно при использовании традиционных методов сварки.

На рисунке показан характер разрушения сварного соединения. При традиционной сварке образец разрушается по шву (а), при использовании разработанной технологии образец разрушился вдали от шва по основному металлу (б). 

 

Макроструктура сварных соединений образцов (x5): 

а – традиционная сварки без предварительной обработки, б – новая технология лазерной сварки с деформированием шва (б – ε= 13 %);  стрелки – границы сварного шва (вид сбоку) после травления в реактиве Келлера

 

Ответственные исполнители: д.ф.-м.н. Оришич А.М., к.т.н. Маликов А.Г., д.ф.-м.н. Черепанов А.Н. (2015 г.).

 

4. Экспериментально установлена возможность повышения механических и эксплуатационных свойств поверхности инструментальной углеродистой стали У8 с помощью лазерной обработки ее поверхности с использованием дисперсной наномодифицирующей композиции, содержащей в качестве матрицы интерметаллид NiAl с добавкой тугоплавких нанопорошков (TiN, Ti_xС_yN, Y₂O₃, или их смеси). Применение нанодисперсных тугоплавких соединений в количестве менее 0,1 % по массе, находящихся в интерметаллидной матрице, позволяет увеличить твердость покрытия в 2–2,5 раза, а износостойкость в 1,4 по сравнению с исходным металлом. Глубина проплавленного слоя составляет примерно 2 мм. Новизна решения заключается в применении наноструктурированных композиций, содержащих нанодисперсные тугоплавкие соединения в интерметаллической матрице. 

        

а                                                                    б

Микротвердость по глубине слоя (а) и морфология (б) проплавленного слоя

Ответственные исполнители: г.н.с., д.ф.-м.н. Черепанов А.Н., м.н.с., к.ф.-м.-н. Дроздов В.О., н.с., к.т.н. Маликов А.Г. (2015 г.).

5. На основе анализа экспериментальных данных определены значения параметров модели пластичности и разрушения Джонсона – Кука, описывающих поведение авиационных титановых сплавов ВТ6, ОТ4 и ОТ4-0 при высокоскоростном деформировании, что позволяет использовать их при проектировании корпусов газотурбинных авиадвигателей с целью обеспечения удерживающей способности во избежание катастрофических последствий, вызванных обрывом лопатки вентилятора.

Проведено численное моделирование процессов деформирования и разрушения корпуса вентилятора газотурбинного авиадвигателя при высокоскоростном соударении с имитатором лопатки вентилятора при ее аварийном обрыве. Сравнение с экспериментальными данными показывает хорошее соответствие по остаточным скоростям вылета оборвавшейся лопатки и формам пробитых отверстий. Показано, что в зависимости от материала корпуса, его толщины и скорости обрыва лопатки существует возможность либо пробития корпуса оборвавшейся лопаткой и ее вылет за его пределы, либо локализация оборвавшейся лопатки внутри корпуса. На основе полученных результатов возможно выработать практические рекомендации по выбору материалов корпусов газотурбинных авиадвигателей.  

а	а
б	б
Рис. 1. Пробитие корпуса имитатором лопатки. Результаты эксперимента (а) и расчета (б). Сплав ВТ6. Толщина стенки корпуса 5 мм.	Рис. 2. Локализация имитатора после удара. Результаты эксперимента (а) и расчета (б). Сплав – ОТ4-0. Толщина стенки корпуса 6 мм.

Ответственные исполнители: зав. лаб., к.ф.-м.н. Краус Е.И., н.с., к.ф.-м.н. Бузюркин А.Е. (2014 г.).

6. В рамках малопараметрического уравнения состояния в условиях высоких температур и давлений был реализован термодинамический подход для вычисления температурной зависимости механических характеристик металлов, таких как модуль сдвига, коэффициент Пуассона, модуль Юнга и коэффициент объемного расширения. Все упругие механические параметры вычислялись без привлечения дополнительных констант.

При решении упругопластической задачи используются уравнения сохранения массы, импульса и энергии. В правой части уравнений движения стоят градиенты компонент тензора напряжений, а на главной диагонали – давление. Девиаторная часть тензора напряжений зависит от механических характеристик, которые являются функциями давления и температуры. С ростом давления и температуры в материале изменяются упругие характеристики материала.

С использованием нелинейной зависимости коэффициента Пуассона от давления 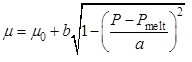 (P_melt – давление, при котором происходит плавление, a и b – параметры, поученные из условия математической непрерывности кривой), была рассчитана продольная скорость звука и получено хорошее соответствие с экспериментальными данными вплоть до температуры плавления. 

Продольная скорость звука для урана

 

Модуль сдвига для урана

 

По полученным скоростям звука объемной и продольной определены все упругие механические характеристики.  На рисунке представлены результаты расчета немонотонного поведения модуля сдвига урана, которые обеспечивают правильную асимптотику при достижении температуры плавления.

Ответственный исполнитель: зав. лаб., к.ф.-м.н. Е.И. Краус (2013 г.).

 

 

 

1. Черепанова В.К., Черепанов А.Н., Шарапов В.Н. Модели динамики фазовых превращений в магматических системах и металлических сплавах. Новосибирск: Изд-во НГТУ, 2015. 243 с. ISBN: 978-5-7782-2761-3

2. Оришич А.М., Черепанов А.Н., Шапеев В.П., Пугачева Н.Б. Наномодифицирование сварных соединений при лазерной сварке металлов и сплавов. Новосибирск: Изд-во СО РАН, 2014. 252 с.

3. Isaev V.I., Cherepanov A.N., Shapeev V.P. Numerical study of Heat Modes of laser welding of dissimilar metals with an intermediate insert // International Journal of Heat and Mass Transfer. 2016. Vol. 99. P. 711–720. DOI: 10.1016/j.ijheatmasstransfer.2016.04.019

4. Buzyurkin A.E., Gladky I.L., Kraus E.I. Determination and verification of Johnson – Cook model parameters at high-speed deformation of titanium alloys // Aerospace Science and Technology. 2015. Vol. 45. P. 121–127. DOI: 10.1016/j.ast.2015.05.001

5. Cherepanov A.N., Mali V.I., Maliutina Iu.N., Orishich A.M., Malikov A.G., Drozdov V.O. Laser welding of stainless steel to titanium using explosively welded composite inserts // International Journal of Advanced Manufacturing Technology. 2017. Vol. 90, No. 9–12. P. 3037–3043. DOI: 10.1007/s00170-016-9657-2

6. Meleshko S.V., Shapeev V.P. Nonisentropic solutions of simple wave type of the gas dynamics equations // Journal of Nonlinear Mathematical Physics. 2011. Vol. 18, No. Suppl. 1. P. 195–212. DOI: 10.1142/S1402925111001374

7. Buzyurkin A.E., Gladky I.L., Kraus E.I. Determination of parameters of the Johnson – Cook model for the description of deformation and fracture of titanium alloys // Journal of Applied Mechanics and Technical Physics. 2015. Vol. 56, No. 2. P. 330-336. DOI: 10.1134/S0021894415020194

8. Popov V.N., Cherepanov A.N., Shchukin V.G. Simulation of metal surface layer modification by nano-particles upon pulsed induction heating // Herald of the Bauman Moscow State Technical University, Series Natural Sciences. 2018. No. 2. P. 82–96. DOI: 10.18698/1812-3368-2018-2-82-96

9. Popov V.N., Cherepanov A.N. Numerical evaluation of the laser-pulse modification modes of the metal surface layer in the presence of a surface-active component in the melt // Thermophysics and Aeromechanics. 2017. Vol. 24, No. 5. P. 779–786. DOI: 10.1134/S0869864317050134

10. Cherepanov A.N., Shapeev V.P., Isaeva V.I. Simulation of heat transfer processes in laser welding of dissimilar metals with an insert // High Temperature. 2015. Vol. 53, No. 6. P. 841–846. DOI: 10.1134/S0018151X15050089

11. Shchukin V.G., Marusin V.V. Induction boriding of steels // Inorganic Materials: Applied Research. 2015. Vol. 6, No. 4. P. 382–387. DOI: 10.1134/S2075113315040218

12. Bublik V.V. Differentially invariant solutions of equations of plane steady flows of a viscous heat-conducting perfect gas with a polytropic equation of state // Journal of Applied Mechanics and Technical Physics. 2012. Vol. 53, No. 2. P. 156–161. DOI: 10.1134/S0021894412020022

13. Shmagunov O.A. Modeling of jet flows of a viscous fluid by the discrete vortex method // Journal of Applied Mechanics and Technical Physics. 2012. Vol. 53, No. 1. P. 20–26. DOI: 10.1134/S0021894412010038

14. Kraus E.I., Shabalin I.I. Melting behind the front of the shock wave // Thermal Science. 2019. Vol. 23, No. 2. P. 519–524. DOI: 10.2298/TSCI19S2519K

15. Buzyurkin A.E., Kraus E.I., Lukyanov Y.L. The shock wave compaction of ceramic powders // Thermal Science. 2019. Vol. 23, No. 2. P. 471–476. DOI: 10.2298/TSCI19S2471B

Нанотехнологии в микро- и макрометаллургических процессах